Le théorème des accroissements finis, en particulier de Rolle, est l’une des pierres angulaires du calcul différentiel. Il offre un aperçu profond de la relation entre la dérivée d’une fonction et les taux de variation locaux, tout en fournissant des outils essentiels pour comprendre les propriétés des fonctions continues et différentiables. Popularisé par le mathématicien français Augustin-Louis Cauchy au 19e siècle, ce théorème est une illustration puissante de la magie de la dérivation
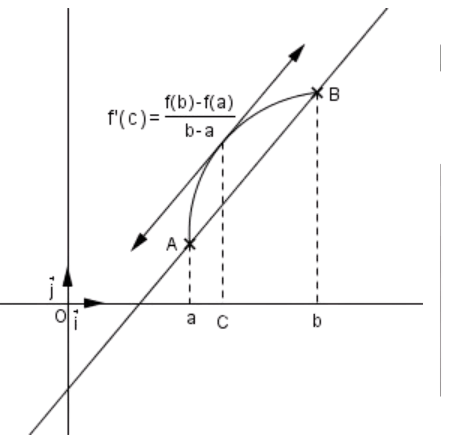
Interprétation géométrique du théorème des accroissements finis: Géométriquement, le théorème dit que quelque part entre les points A et B sur une courbe différentiable, il y a au moins une ligne tangente parallèle à la ligne sécante AB. Des application de ce theoreme sont regrouper dans la parties exercices sur les fonctions dérivables.
Théorème des accroissements finis pour les fonctions à valeurs réelles
Enoncé et interprétation géométrique du théorème
Théorème: Soit $a,b\in\mathbb{R}$ tels que $b>a$ et $f:[a,b]\to\mathbb{R}$ une fonction continue sur l’intervalle fermé $[a,b]$ et dérivable sur l’intervalle ouvert $]a,b[$. Alors il existe $c\in ]a,b[$ tel que \begin{align*} f'(c)=\frac{f(b)-f(a)}{b-a}.\end{align*}
Intuitivement, cela signifie qu’à un moment donné dans l’intervalle $]a,b[,$ la pente de la tangente à la courbe de $f$ est égale à la pente de la ligne reliant les points$(a,f(a))$ et $ (b,f(b))$.
Pour mieux comprendre ce théorème, imaginons une voiture parcourant une route sinueuse. Si la voiture atteint la même position finale qu’initiale, alors à un moment donné, sa vitesse instantanée doit avoir été égale à sa vitesse moyenne sur tout le trajet. En d’autres termes, il y a eu un point où la voiture a roulé à la même vitesse que sa vitesse moyenne.
Exercice: Montrer que pour tout $t,s\in\mathbb{R}^+,$ on a \begin{align*} |\sin(\sqrt{t})-\sin(\sqrt{s})|\le |t-s|^{\frac{1}{2}}.\end{align*}
Soit $x,y\in\mathbb{R}^+$ (on peut supposer $y>x$). L’application $\sin: [x,y]\to \mathbb{R}$ est continue et dérivable sur $[x,y]$. Donc selon le theoreme des accroissements finis, il existe $c\in ]x,y[$ tel que $\sin(y)-\sin(x)=\cos(c)(y-x)$. Cela implique que $|\sin(y)-\sin(x)|\le |y-x|$ pour tout $x,y\in\mathbb{R}^+$. En particulier pour $y=\sqrt{t}$ et $x=\sqrt{s}$ pour $t,s\in \mathbb{R}^+$, on a \begin{align*}|\sin(\sqrt{t})-\sin(\sqrt{s})|\le |\sqrt{t}-\sqrt{s}|\le |t-s|^{\frac{1}{2}}.\end{align*}Consulter aussi les fonctions höldériennes.
Théorème de Rolle
Le théorème suivant, dit théorème de Rolle, est un cas particulier du théorème des accroissement finis.
Théorème (Rolle): Soit $a,b\in\mathbb{R}$ tels que $b>q$ et $f:[a,b]\to\mathbb{R}$ une fonction continue sur l’intervalle fermé $[a,b]$ et dérivable sur l’intervalle ouvert $]a,b[$ tel que $f(a)=f(b)$. Alors il existe $c\in ]a,b[$ tel que $f'(c)=0$.
Visuellement, le théorème de Rolle peut être compris comme suit : imaginez une courbe continue qui commence et finit au même niveau. Si cette courbe n’a pas de points plats (où la pente est horizontale), alors elle doit nécessairement avoir au moins un point où sa pente (représentée par la dérivée) est nulle. Cela signifie qu’il existe un point où la courbe se « repose » temporairement avant de monter ou de descendre.

Exercice: Soit $P$ un polynôme à $n$ racines réelles distinctes deux à deux. Montrer que le polynôme dérivé $P’$ a exactement $n-1$ racines distinctes.
On note par $\lambda_1,\cdots,\lambda_n$ les $n$ racines réelles de $P$ tel que $\lambda_i\neq \lambda_j$ pour tout $i,j\in\{1,2,\cdots,n\}$. Sans perdre de généralités, on peut supposer que $\lambda_1<\lambda_2<\cdots<\lambda_n$. pour tout $i\in \{1,2,\cdots,n-1\}$, $x\mapsto P(x)$ est continue est dérivable sur $[\lambda_i,\lambda_{i+1}]$ et que $P(\lambda_i)=P(\lambda_{i+1})=0$. Selon le théorème de Rolle, il existe $c_i\in ]\lambda_i,\lambda_{i+1}[$ tel que $P'(c_i)=0$. Ainsi on a $n-1$ racines réelles distincts pour le polynôme $P'$.
Inégalité des accroissements finis
Théorème: Soit $m,n\in\mathbb{N}^\ast$, $\mathscr{U}$ un ouvert de $\mathbb{R}^n$ et $f:\mathscr{U}\to \mathbb{R}^m$ une fonction différentiable sur $\mathscr{U}$. Soint $x,y\in \mathscr{U}$ tel que le segment $[x,y]:=\{tx+(1-t)y: t\in [0,1]\}\in \mathscr{U}$. Si la différentielle $Df:\mathscr{U}\to\mathscr{M}_{m,n}(\mathbb{R})$ est bornee sur le segment $[x,y]$, alors \begin{align*} \|f(x)-f(y)\|\le M \|x-y\|\end{align*} avec $M=\sup_{h\in [x,y]}\|Df(h)\|$.
L’inégalité des accroissements finis a des applications significatives en mathématiques, en sciences et en ingénierie. Elle permet de dériver d’autres inégalités importantes, comme l’inégalité de Cauchy-Schwarz et l’inégalité triangle. Elle est également utilisée pour prouver des résultats sur la convergence des séries et des fonctions.
Dans l’analyse numérique, cette inégalité est utilisée pour justifier des méthodes d’approximation et d’itération. En économie, elle peut être appliquée pour modéliser et estimer les taux de croissance et les taux de variation.
Avec cette inégalité, on peut montrer que tout function de classe $C^1$ sur un ouvert est localement Lipschitzienne. C’est une condition tres importante dans la théorie des équations différentielles non-linéaires.
Applications et Conséquences
Le théorème des accroissements finis a des implications importantes dans de nombreux domaines des mathématiques et des sciences. Il sert de base à la preuve du théorème des valeurs intermédiaires et du théorème de Rolle, et il est également utilisé pour établir le développement de Taylor et d’autres résultats clés de l’analyse mathématique.
En économie et en physique, ce théorème peut être utilisé pour analyser les taux de variation et les tendances moyennes. Dans la modélisation mathématique, il est souvent crucial de comprendre comment les grandeurs varient, et le théorème des accroissements finis fournit un outil puissant pour le faire.
En somme, le théorème des accroissements finis est bien plus qu’une simple relation mathématique. Il incarne l’essence même du calcul différentiel en reliant les notions de dérivée, de tangente et de variation, et il continue d’exercer son influence dans divers domaines de la science et de l’ingénierie.
