La trigonométrie est l’étude des relations entre les angles et les côtés des triangles. Les fonctions trigonométriques, telles que le sinus, le cosinus et la tangente, jouent un rôle essentiel dans divers domaines scientifiques et mathématiques.
Les Principaux Concepts de la Trigonométrie
Les Angles et les Mesures Angulaires
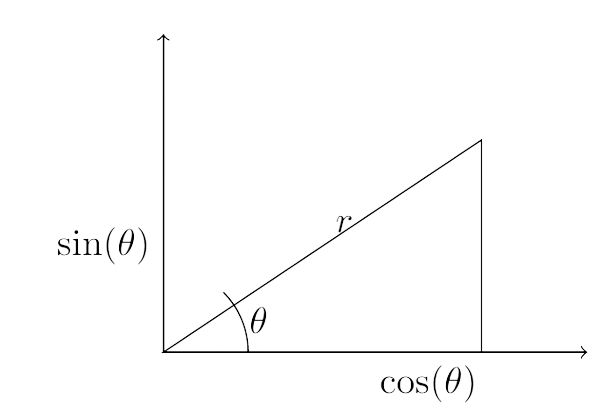
Les angles jouent un rôle fondamental en trigonométrie, servant de base pour comprendre les relations entre les fonctions trigonométriques et les propriétés des triangles. Dans ce contexte, la mesure des angles devient une compétence essentielle.
Les angles sont généralement mesurés en degrés, avec un tour complet correspondant à 360 degrés. Cependant, pour des calculs plus avancés, les radians sont souvent utilisés comme unité de mesure. Un radian est défini comme l’angle subtendu au centre d’un cercle lorsque l’arc de longueur égale au rayon est parcouru. Une particularité intéressante est que le cercle complet correspond à $2\pi$ radians. La transition entre les mesures en degrés et en radians est cruciale pour comprendre la manière dont les angles interagissent avec les fonctions trigonométriques et la géométrie, formant ainsi le socle sur lequel repose la compréhension approfondie de la trigonométrie.
Le Cercle Trigonométrique
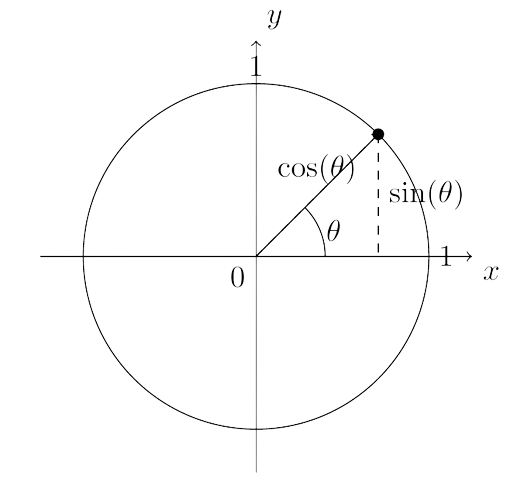
Le cercle trigonométrique est un outil graphique puissant utilisé en trigonométrie pour visualiser les relations entre les angles et les fonctions trigonométriques. Il consiste en un cercle unitaire centré à l’origine d’un système de coordonnées. En utilisant ce cercle, nous pouvons représenter graphiquement les valeurs des fonctions trigonométriques en fonction des angles.
Soit $\theta$ un angle en radians. Si nous traçons un rayon à partir de l’origine faisant un angle $\theta$ avec l’axe des abscisses, le point d’intersection de ce rayon avec le cercle aura des coordonnées $(\cos(\theta),\sin(\theta))$. Ces coordonnées sont directement liées aux fonctions trigonométriques du cosinus et du sinus de l’angle $\theta$. Ainsi, le cercle trigonométrique fournit une manière visuelle de comprendre comment les valeurs de $\cos(\theta)$ et $\sin(\theta)$ varient en fonction de l’angle $\theta$.
De plus, le cercle trigonométrique permet de dériver des identités trigonométriques importantes. Par exemple, l’identité fondamentale $\cos^2(\theta)+\sin^2(\theta)=1$ peut être déduite à partir de la distance entre le point $(\cos(\theta),\sin(\theta))$ sur le cercle et l’origine.
En résumé, le cercle trigonométrique est un outil visuel qui établit une connexion entre les angles, les fonctions trigonométriques et la géométrie. Les formules $(\cos(\theta),\sin(\theta))$ permettent d’associer chaque angle à un point sur le cercle, facilitant ainsi la compréhension des relations fondamentales de la trigonométrie.
Les Fonctions Trigonométriques de Base
Les fonctions trigonométriques de base, à savoir le sinus ($\sin$), le cosinus ($\cos$) et la tangente ($\tan$), forment le cœur de la trigonométrie. Ces fonctions sont étroitement liées aux mesures des angles et aux propriétés des triangles, et elles jouent un rôle crucial dans de nombreux domaines mathématiques et scientifiques.
Le sinus d’un angle dans un triangle est défini comme le rapport entre la longueur du côté opposé à l’angle et la longueur de l’hypoténuse (le côté le plus long). Mathématiquement, pour un angle $\theta$ le sinus est donné par
$$ \sin(\theta)=\frac{\text{côté opposé}}{\text{hypotènuse}}.$$
Le sinus varie entre -1 et 1, atteignant son maximum lorsque l’angle est de 90 degrés (ou $\frac{\pi}{2}$ radians).
Le cosinus d’un angle dans un triangle est défini comme le rapport entre la longueur du côté adjacent à l’angle et la longueur de l’hypoténuse. Pour un angle $\theta$ le cosinus est donné par
$$ \cos(\theta)=\frac{\text{côté adjacent}}{\text{hypotènuse}}.$$
Le cosinus varie également entre -1 et 1, atteignant son maximum lorsque l’angle est de 0 degré (ou $2\pi$ radians) et son minimum lorsque l’angle est de 180 degrés (ou $\pi$ radians).
La tangente d’un angle dans un triangle est définie comme le rapport entre le sinus de l’angle et le cosinus de l’angle. Mathématiquement, pour un angle $\theta$ qui n’est pas congru à $\frac{\pi}{2}$ modulo $\pi$, la tangente est donnée par
$$ \tan(\theta)=\frac{\sin(\theta)}{\cos(\theta)}.$$
| $\theta$ | $0$ | $\frac{\pi}{6}$ | $\frac{\pi}{4}$ | $\frac{\pi}{3}$ | $\frac{\pi}{2}$ |
| $\cos(\theta)$ | $1$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | $0$ |
| $\sin(\theta)$ | $0$ | $\frac{1}{2}$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{3}}{2}$ | $1$ |
| $\tan(\theta)$ | $0$ | $\frac{\sqrt{3}}{2}$ | $1$ | $\sqrt{3}$ | non défini |
Variations des fonctions trigonométriques
Les fonctions $x\mapsto \sin(x)$ et $x\mapsto \cos(x)$ sont definies, continues et dérivables sur tout $\mathbb{R}$. De plus, pour tout $x\in\mathbb{R}$,
$$ \sin'(x)=\cos(x)\quad\text{et}\quad \cos'(x)=-\sin(x).$$
La fonction $x\mapsto \tan(x)$ et definie, continue et dérivable sur $\mathbb{R}\setminus\{\frac{(2k+1)\pi}{2}\}.$ De plus on a
$$ \tan'(x)=1+\tan^2(x).$$
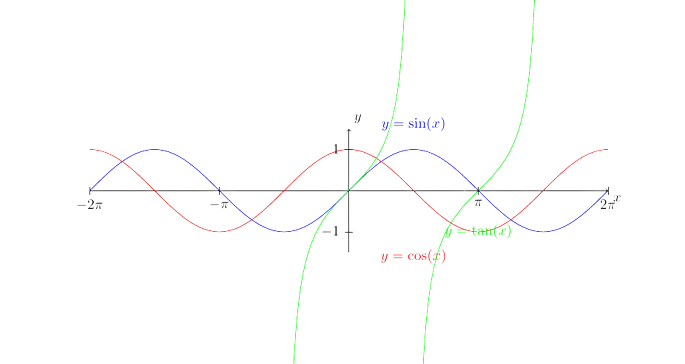
Ces fonctions trigonométriques de base sont utilisées pour modéliser des phénomènes périodiques, résoudre des triangles, analyser les mouvements circulaires et plus encore. Leur compréhension est essentielle pour naviguer efficacement dans les domaines de la géométrie, de la physique, de l’ingénierie et d’autres disciplines où les angles et les cycles jouent un rôle central.
Parité, symétrie et valeurs
Les fonctions sinus et cosinus sont des exemples de fonctions trigonométriques périodiques qui exhibent des propriétés de parité et de symétrie intéressantes. La fonction sinus est impaire, ce qui signifie que $\sin(−x)=−\sin(x)$, reflétant une symétrie centrale par rapport à l’origine. D’autre part, la fonction cosinus est paire, c’est-à-dire que $\cos(−x)=\cos(x)$, montrant une symétrie axiale par rapport à l’axe des ordonnées. Ces propriétés de parité et de symétrie sont essentielles pour simplifier les expressions trigonométriques et comprendre les variations des fonctions sur tout leur domaine.
| $\beta$ | $-\theta$ | $\theta+\pi$ | $\theta-\pi$ | $\theta+2\pi$ | $\frac{\pi}{2}-\theta$ | $\frac{\pi}{2}+\theta$ |
| $\cos(\beta)$ | $\cos(\theta)$ | $-\cos(\theta)$ | $-\cos(\theta)$ | $\cos(\theta)$ | $\sin(\theta)$ | $-\sin(\theta)$ |
| $\sin(\beta)$ | $-\sin(\theta)$ | $-\sin(\theta)$ | $\sin(\theta)$ | $-\sin(\theta)$ | $\cos(\theta)$ | $\cos(\theta)$ |
Relations Trigonométriques et Identités
Les identités trigonométriques jouent un rôle central dans la simplification et la résolution d’équations trigonométriques complexes. Ces relations mathématiques permettent de transformer les expressions trigonométriques en d’autres formes équivalentes, facilitant ainsi les calculs et les manipulations. Voici quelques-unes des identités les plus fondamentales et utiles en trigonométrie :
Identités Trigonométriques Fondamentales
La relation la plus célèbre est $$\cos^2(\theta)+\sin^2(\theta)=1,$$ qui établit une relation entre les carrés du sinus et du cosinus d’un angle. Cette identité est basée sur le théorème de Pythagore appliqué à un triangle rectangle. D’autres identités fondamentales incluent $$ \tan^2(x)=1+\sec^2(x),\quad 1+\cot^2(x)=\csc^2(x)$$ avec $$ \csc(x)=\frac{1}{\sin(x)},\; \sec(x)=\frac{1}{\cos(x)},\; \cot(x)=\frac{1}{\tan(x)}.$$
Identités de Somme et de Différence
Ces identités relient les valeurs des fonctions trigonométriques pour la somme ou la différence de deux angles.
Des formules pour sinus
\begin{align*} & \sin(x+y)=\sin(x)\cos(y)+\sin(y)\cos(x),\cr & \sin(x-y)=\sin(x)\cos(y)-\sin(y)\cos(x).\end{align*} En particulier si $x=y$, on a $$ \sin(2x)=2 \sin(x)\cos(x).$$
Des formules pour cosinus
\begin{align*} & \cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y),\cr & \cos(x-y)=\cos(x)\cos(y)+\sin(x)\sin(y).\end{align*} En particulier si $x=y$, on a $$ \cos(2x)=2\cos^2(x)-1=1-2\sin^2(x).$$
Des formules pour la fonction tangente
\begin{align*} & \tan(x+y)=\frac{\tan(x)+\tan(y)}{1-\tan(x)\tan(y)},\cr & \tan(x-y)=\frac{\tan(x)-\tan(y)}{1+\tan(x)\tan(y)}.\end{align*} En particulier si $x=y$, on a $$ \tan(2x)=\frac{2\tan(x)}{1-\tan^2(x)}.$$
Formules de factorisation :
Si on pose $$ a=\frac{x+y}{2},\quad b=\frac{x-y}{2},$$ alors on a $a+b=x$ et $a-b=y$. Donc si on applique les formules trigonométriques déjà vues plus haut, on retrouve les formules de factorisation suivantes
\begin{align*} & \cos(x)+\cos(y)=2\cos\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right),\cr & \cos(x)-\cos(y)=-2\sin\left(\frac{x+y}{2}\right)\sin\left(\frac{x-y}{2}\right).\end{align*}
\begin{align*} & \sin(x)+\sin(y)=2\sin\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right),\cr & \sin(x)-\sin(y)=2\sin\left(\frac{x-y}{2}\right)\cos\left(\frac{x+y}{2}\right).\end{align*}
La maîtrise de ces identités et de leurs applications permet de simplifier les expressions trigonométriques, de résoudre des équations trigonométriques complexes et d’analyser des modèles périodiques. Ces outils sont essentiels pour explorer des domaines allant de l’algèbre avancée à la physique et à l’ingénierie, où la trigonométrie joue un rôle clé dans la modélisation et la résolution de problèmes réels.
Relation avec les nombres complexes
Les fonctions trigonométriques, telles que le sinus et le cosinus, sont étroitement liées aux nombres complexes et jouent un rôle important dans la représentation et la manipulation de ces nombres. Les nombres complexes peuvent être exprimés sous forme trigonométrique, ce qui permet de les visualiser et de les opérer plus efficacement.
En utilisant la formule d’Euler, $$ e^{i\theta}=\cos(\theta)+\imath\sin(\theta),$$
où $\imath$ est l’unité imaginaire, les fonctions trigonométriques sont étendues aux nombres complexes. Cette formule relie les fonctions exponentielles et trigonométriques d’une manière profonde. Elle permet de représenter un nombre complexe $z$ sous la forme $z=re^{\imath \theta},$ où $r$ est le module de $z$, et $\theta$ est l’argument de $z$ (l’angle que le vecteur complexe forme avec l’axe des réels positifs).
De plus, les propriétés trigonométriques, comme les identités trigonométriques, sont également valides pour les nombres complexes. Les relations trigonométriques permettent de simplifier les calculs impliquant des fonctions trigonométriques de nombres complexes, facilitant ainsi l’analyse et la résolution de problèmes complexes dans divers domaines.
En résumé, les fonctions trigonométriques et les nombres complexes sont étroitement interconnectés, ce qui offre une perspective unifiée pour comprendre et manipuler des quantités mathématiques dans des contextes variés, allant de la géométrie à l’analyse complexe et aux applications en physique et en ingénierie.
Exercices sur les nombres complexes et trigonométrie
Les exercices suivants sur les nombres complexes et trigonométrie s’adressent aux élèves du baccalauréat scientifique.
Exercice:
- Trouver les nombres complexes $z_1$ et $z_2$ vérifiant la relation:\begin{align*}z_1z_2=i,\qquad z_1-z_2=1+i.\end{align*}
- Mettre $z_1$ et $z_2$ sous forme trigonométrique.
Solution:
- Dans cette question il faut bien faire attention et de ne pas se lancer dans des calcul horrible. En effet, il serait maladroit de déterminer $z_1$ en fonction de $z_2,$ puis de reporter l’expression de $z_1$ dans la deuxième équation. Nous allons présenter une autre méthode plus courte et plus élégante: On a\begin{align*}\begin{cases} z_1 z_2=i\cr z_1-z_2=1+i\end{cases}\;\Longleftrightarrow\;\begin{cases} z_1 (-z_2)=i\cr z_1+(-z_2)=1+i.\end{cases}\end{align*}Donc $z_1$ et $(-z_2)$ sont solution de l’équation:\begin{align*}\tag{E}t^2-(1+i)t-i=0.\end{align*}Le discriminant associé a cette équation est\begin{align*}\Delta&= 2i+4i=6i\cr &= \left(\sqrt{6}\left(\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2} i\right)\right)^2.\end{align*}Donc $Delta$ admet pour racines carrées:\begin{align*}\Delta_1=\sqrt{3}+\sqrt{3}i\quad \text{et}\quad \Delta_2=-\sqrt{3}-\sqrt{3}i.\end{align*}Les racines de l’équation $(E)$ sont donc\begin{align*}\lambda_1&=\frac{1+i+\Delta_1}{2}\cr &= \frac{1+\sqrt{3}}{2}(1+i)\end{align*} et \begin{align*}\lambda_2&=\frac{1+i+\Delta_2}{2}\cr &= \frac{1-\sqrt{3}}{2}(1+i).\end{align*}Ainsi on $z_1=\lambda_1$ et $-z_2=\lambda_2$ ou $z_1=\lambda_2$ et $-z_2=\lambda_1$. D’où les solutions du système sont les couples $(\lambda_1,-\lambda_2)$ et $(\lambda_2,-\lambda_1),$ soit\begin{align*}&\left(\frac{1+\sqrt{3}}{2}(1+i), \frac{\sqrt{3}-1}{2}(1+i)\right),\;\text{et}\cr&\left(\frac{1-\sqrt{3}}{2}(1+i),\frac{-1-\sqrt{3}}{2}(1+i)\right).\end{align*}
