Les fonctions uniformément continues sont un concept fondamental en analyse mathématique, particulièrement dans l’étude des propriétés des fonctions réelles. Dans cet article, nous plongerons dans les subtilités de ces fonctions et explorerons leurs caractéristiques clés ainsi que leur importance dans divers domaines mathématiques.
Classe des fonctions uniformément continues
L’idée de continuité joue un rôle central dans l’analyse mathématique. Une fonction est dite continue en un point si elle ne présente pas de sauts brusques ou de discontinuités. Cependant, il existe des situations où une continuité plus « lisse » est requise. C’est là qu’interviennent les fonctions uniformément continues.
Une fonction $f:I\subset \mathbb{R}\to \mathbb{R}$ est uniformément continue sur $I$ si pour tout $\varepsilon>0$, il existe $\delta>0$ tel que pour tout $x,y\in I$, si $|x-y| < \delta,$ alors $|f(x)-f(y)| < \varepsilon$.
L’idée clé ici est que le même $\delta$ fonctionne pour tous les points de l’intervalle, indépendamment de leur position. Contrairement à la continuité habituelle où $\delta$ dépend généralement de $x$, dans le cas de la continuité uniforme, $\delta$ dépend uniquement de $\varepsilon$.
Propriétés et Exemples
On a les remarques suivantes
- Toute fonction uniformément continue est continue. Porter l’inverse n’est pas vrai. En effet on peut construire des exemples de fonctions continues, sans être uniformément continues.
- Tout fonction continue sur un compact est uniformément continue. De plus elle est bornée, c’est le théorème de Heine-Borel.
- Toute fonction lipschitzienne est uniformément continues.
- La composition de fonctions uniformément continues reste uniformément continue
Les fonctions uniformément continues jouent un rôle essentiel dans divers domaines des mathématiques et de la physique. Elles sont souvent utilisées pour garantir des propriétés de stabilité et de convergence dans les équations différentielles, les séries de fonctions et les équations intégrales.
Graphe d’une fonction uniformément continue
Le graphe d’une fonction uniformément continue est une représentation visuelle de la manière dont la fonction se comporte sur son domaine en respectant la propriété d’uniforme continuité. Contrairement aux fonctions simplement continues, les fonctions uniformément continues montrent moins de fluctuations brusques et abruptes sur leurs graphiques. Les variations entre les valeurs des points du graphe sont régulières, même lorsque les distances entre les points sont très proches.
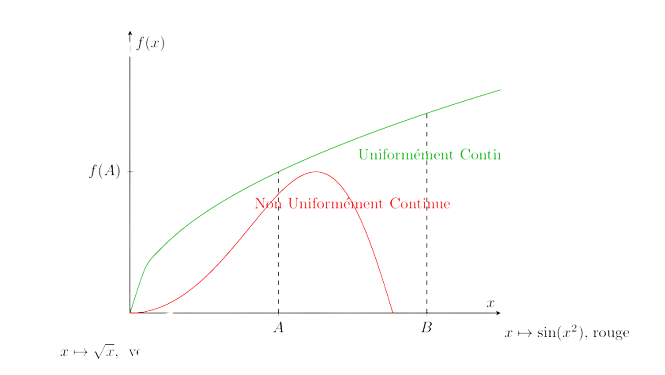
Dans un graphe de fonction uniformément continue, vous pouvez vous attendre à observer des transitions plus douces et moins abruptes entre les valeurs de la fonction. Cela signifie que même si vous choisissez des points très proches sur le graphe, les valeurs correspondantes de la fonction ne varieront pas brusquement, ce qui est conforme à la définition de la continuité uniforme.
En résumé, le graphe d’une fonction uniformément continue présente des variations régulières et progressives entre les valeurs, reflétant la nature lisse de la continuité uniforme.
Exercises corrigés
Nous donnons quelques exercices classique sur la continuité uniforme des fonctions.
Uniforme continuité et limite de fonctions
Exercice 1: ⭐⭐⭐⭐ Soit $f:\mathbb{R}^+\to \mathbb{R}$ une fonction uniformément continue sur $\mathbb{R}^+$. On suppose que pour tout entier $p\in \mathbb{N}^\ast,$ la suite\begin{align*}\left( f\left(\frac{n}{p}\right)\right)_{n\in\mathbb{N}}\end{align*}est convergente.
- Montrer que $\ell$ la limite de cette suite est est independant du choix $p$.
- Montrer que $f(x)$ a une limite lorsque $x$ tend vers $+\infty$
- Soient $p$ et $q$ deux entiers dans $\mathbb{N}^ast$. Soient $\ell_p$ et $\ell_q$ les limite, respectives, des suites $(v_n)_n=(f(n/p))_n$ et $(w_n)_n=(f(n/p))_n$. On définit les fonctions strictement croissantes\begin{align*}&\varphi: \mathbb{N}\to \mathbb{N},\quad \varphi(n)=n/p\cr &\psi: \mathbb{N}\to \mathbb{N},\quad \varphi(n)=n/q.\end{align*}Alors $(v_{\varphi(n)})_n$ et $(w_{\psi(n)})_n$ sont deux sous-suites de $(v_n)_n$ et $(w_n)_n,$ respectivement. Donc\begin{align*}\lim_{n\to+\infty}v_{\varphi(n)}=\ell_p,\quad \lim_{n\to+\infty}w_{\psi(n)}=\ell_p.\end{align*}Remarquons, ensuite, que pour tout $n\in\mathbb{N}$ on a\begin{align*}v_{\varphi(n)}=f(n/pq)=w_{\psi(n)}.\end{align*}Ainsi $\ell_p=\ell_q$.
- Nous allons montrer que pour tout $\varepsilon > 0$, il existe $A>0$ tel que pour tout $x>A$ on a $|f(x)-\ell| < \varepsilon$. En effet, comme $f$ est uniformément continue sur $\mathbb{R}^+,$ pour tout $\varepsilon > 0$ il existe $\alpha >0$ tel que pour tout $x,y\in\mathbb{R}^+$, si $|x-y| \le \alpha$ alors $|f(x)-f(y)|\le \varepsilon/2$. Soit $p$ un entier tel que $p > 1/\alpha$. D’après la question, il existe $N\in\mathbb{N}$ tel que pour tout $n\ge N$ on a $|f(n/p)-\ell|\le \varepsilon/2$. Soit maintenant $x>N/p$. Si on pose $n_0=E(xp)$ alors on a $n_0\le xp < n_0+1$. Donc\begin{align*}0 \le x-\frac{n_0}{p} < \frac{1}{p} < \alpha.\end{align*}Ce qui implique que\begin{align*}|f(x)-f(\frac{n_0}{p})|\le \varepsilon/2.\end{align*}D’autre part, on a $n_0\ge N$, donc $|f(\frac{n_0}{p})-\ell|\le \varepsilon/2$. Ainsi pour $x\ge A=\frac{N}{p}$, on a\begin{align*}|f(x)-\ell|\le |f(x)-f(\frac{n_0}{p})|+|f(\frac{n_0}{p})-\ell|\le \varepsilon/2.\end{align*}D’où le résultat.
Une fonction continue, mais pas uniformément continue
Exercice:
- Montrer que $f:\mathbb{R}\to \mathbb{R}$ n’est pas uniformément continue si et seulement si il existe deux suite $(x_n)_n$ et $(y_n)_n$ tel que la suite $(x_n-y_n)_n$ tende vers zéro et que la suite $(|f(x_n)-f(y_n)|)_n$ soit minorée.
- Montrer que la fonction $f(x)=\sin(x^2),\;x\in\mathbb{R},$ n’est pas uniformément continue sur $\mathbb{R}$.
- $f$ est uniformément continue sur $\mathbb{R}$ si et seulement si pour tout $\varepsilon >0,$ il existe $\alpha > 0$ tel que pour tout $x,y\in\mathbb{R}$, $|x-y| \le \alpha$ implique que $|f(x)-f(y)|\le \varepsilon$. Par contraposition $f$ n’est pas uniformément continue si et seuelement si il existe $\varepsilon >0,$ tel que pour $\alpha > 0$, il exists $x_\alpha,y_\alpha\in\mathbb{R}$ tel que $|x_\alpha -y_\alpha| \le \alpha$ et $|f(x_\alpha)-f(y_\alpha)|>\varepsilon$. En particulier, pour tout $n\in\mathbb{N}^\ast,$ on pose $\alpha=\frac{1}{n}$, et donc il existe deux suites $(x_n)_n,(y_n)_n\subset \mathbb{R}$ telles que $|x_n-y_n|\le \frac{1}{n}$ et $|f(x_n)-f(y_n)|>\varepsilon$, pour tout $n$. Ceci montre que $|x_n-y_n|$ tende vers $0$ quand $n\to+\infty$ et que la suite $(|f(x_n)-f(y_n)|)_n$ est minorée.
- Pour montrer que la fonction $f(x)=\sin(x^2)$ n’est pas uniformément continue sur $\mathbb{R}$, on choisit les suites suivantes\begin{align*}x_n= \sqrt{n\pi},\qquad y_n=\sqrt{(n+\frac{1}{n})\pi},\qquad n\in\mathbb{N}.\end{align*} On a \begin{align*}x_n-y_n&=\sqrt{n\pi}-\sqrt{(n+\frac{1}{n})\pi}\cr &= \frac{\frac{\pi}{2}}{\sqrt{n\pi}+\sqrt{(n+\frac{1}{n})\pi}}.\end{align*}Ce qui implique que $x_n-y_n\to 0$ quand $n\to +\infty$. D’autre part, on a\begin{align*}|f(x_n)-f(y_n)|&=|\sin(n\pi)-\cos(n\pi)|\cr &= |0-(-1)^n|=1.\end{align*}Donc d’après la question 1, la fonction $x\mapsto \sin(x^2)$ n’est pas uniformément continue.
Conclusion
En conclusion, les fonctions uniformément continues sont un outil puissant pour étudier la continuité en dehors du contexte habituel. Elles assurent une douceur constante dans le comportement des fonctions sur tout un intervalle. Comprendre cette notion est essentiel pour explorer des concepts plus avancés en analyse mathématique et pour résoudre des problèmes concrets dans diverses disciplines.
Que vous soyez un étudiant en mathématiques, en physique ou dans un autre domaine, la compréhension des fonctions uniformément continues ouvre la porte à des applications et des découvertes passionnantes.
